ALGORITMA PENGURUTAN DATA

      A. Selection Sort

  Algoritma selection sort dapat dirangkum sebagai berikut
 1. Temukan nilai yang paling minimum (atau sesuai keinginan) di dalam struktur data.  Jika ascending, maka yang harus ditemukan adalah nilai yang paling minimum. Jika descending, maka temukan nilai yang paling maksimum.
2. Tukar nilai tersebut dengan nilai pada posisi pertama di bagian struktur data yang  belum diurutkan
3. Ulangi langkah di atas untuk bagian struktur data yang tersisa.

Script program:

/*Selection Sort*/

#include <iostream>

#include <iomanip>

using namespace std;

void SelectionSort (int array [], const int size)

{

          int i,j,kecil,temp;

          for (i=0; i<size; i++)

                   {

                             kecil=i;

                             for(j=i+1; j<size; j++)

                             {

                                      if (array[kecil]>array[j])

                                      {kecil=j;}

                             }temp= array [i];

                             array[i]=array[kecil];

                             array[kecil]=temp;

                   }

}

int main ()

{

          int NumList[8]={5,34,32,25,75,42,22,2};

          int temp;

          cout<<"Data Sebelum Diurutkan: \n";

          for(int d=0; d<8;d++)

          {

                   cout<<setw(3)<<NumList[d];

          }

          cout<<"\n\n";

          SelectionSort (NumList, 8);

          cout<<"Data Setelah Diurutkan : \n";

          for (int iii=0; iii<8; iii++)

          cout<<setw(3)<<NumList[iii]<<endl<<endl;

}

Contoh Program :

  Algoritma :

1. Mulai.

2. Membaca file header.

3. Membaca fungsi, int, kecil, temp.

4. Membaca perulangan beserta fungsi kecil dan temp.

5. Membaca fungsi utama, fungsi numlist dan temp.

6. Membaca perulangan.

7. Cetak hasil.

8. Tampilan data sebelum diurutkan.

9. Membaca fungsi metode selection sorting.

10. Membaca perulangan.

11. Cetak hasil.

12. Tampilan data setelah diurutkan.

13. Selesai.   

c     B. Exchange Sort

Cara pengurutan exchange sort :

Prosedur Exchange Sort :

void exchange_sort(int data[])
{
for(int i=0;i<n-1;i++)
{
for(int j=i+1;j<n;j++)
{
if(data[i]<data[j])
tukar(&data[i],&data[j]);
}
}
}

-    C. Selection Sort

Contoh simulasi algoritma selection sort sbb :
jika kita memiliki elemen array sbb :  {5, 1, 12, -5, 16, 2, 12, 14}

 

Algoritma di dalam Selection Sort terdiri dari kalang bersarang. Dimana kalang tingkat pertama (disebut pass) berlangsung N-1 kali. Di dalam kalang kedua, dicari elemen dengan nilai terkecil. Jika didapat, indeks yang didapat ditimpakan ke variabel min. Lalu dilakukan proses penukaran. Begitu seterusnya untuk setiap Pass. Pass sendiri makin berkurang hingga nilainya menjadi semakin kecil. Berdasarkan operasi perbandingan elemennya.

implementasinya dalam bahasa pemrograman sbb :

/**
 *
 * @author Edi Zhou
 */
public class selectionSort {

    int[] angka={5, 1, 12, -5, 16, 2, 12, 14};
    public selectionSort()
    {

        tampilkanAngka();
        urutkanAngka();
        tampilkanAngka();
       
    }

    void tampilkanAngka()
    {
        System.out.println(“\n——————————–“);
        for (int i=0;i<angka.length;i++)
        {
            System.out.print(angka[i]+” “);
        }
    }

    void urutkanAngka()
    {
        int tampung;
        for (int i=0;i<angka.length-1;i++)
        {
            int minindek=i;
            for(int j=i+1;j<angka.length;j++)
            {
                if(angka[j]<angka[minindek])
                    minindek=j;

                if(minindek!=i)
                {

                    tampung=angka[i];
                    angka[i]=angka[minindek];
                    angka[minindek]=tampung;
                }           
            }
           
         //tampilkanAngka();
        }

    }

    public static void main(String[] aksi)
    {
        selectionSort urut = new selectionSort();
    }
}

-         Heap Sort

Program Heap Sort :

Source code:

    void siftDown(int arr[], int start, int end) {
    /** start dan end berada dalam jangkauan array yang terdefinisi dengan start < end **/
    /** Menata array dalam jangkauan sesuai kriteria sifat heap **/

    /** deklarasi **/
    int root=start;        // pencarian dimulai dari root
    int child;            // menyimpan indeks anak yang diperiksa
    int inswap;            // indeks untuk swap
    int temp;

    /** sift ketika root masih memiliki anak **/
    /** indeks anak ada di 2*root+1 dan 2*root+2 **/
    while(2*root+1 <= end) {
    child     = 2*root+1;    // dapatkan data anak
    inswap     = root;

    /** Ambil elemen terbesar dan letakkan di root **/
    if(arr[inswap] < arr[child])
    inswap = child;

    if(child+1 <= end)
    if(arr[inswap] < arr[child+1])
    inswap = child+1;

    if(root!=inswap) {
    // pertukarkan
    temp         = arr[root];
    arr[root]     = arr[inswap];
    arr[inswap]    = temp;

    // track down, buat agar struktur heap di bawah konsisten
    root = inswap;
    } else return;
    }
    }

    //————————————————————————————

    void heapify(int arr[], int n) {
    /** n = jumlah elemen di array **/

        /** heapidy membentuk heap dengan bantuan siftdown. Hasil akhirnya adalah array yang tertata sesuai sifat heap **/

    /** mulai heapify dari tengah dan terus naik hingga indeks 0 **/
    int start=(n-2)/2;
    for(int i=start; i>=0; i–)
    siftDown(arr,i,n-1);
    }

    //————————————————————————————

void heapsort(int arr[], int n) {
    /** n = jumlah elemen di array **/

    /** lakukan heapify untuk menciptakan heap semu **/
    heapify(arr,n);

    /** tercipta heap, elemen terbesar ada di root (indeks 0)
    *  lakukan iterasi untuk setiap langkah, pindahkan root ke akhir,
    *  decrement indeks dan lakukan penataan ulang lagi
    */
    int end=n-1;
    int temp;
    while(end>0) {
    // pindahkan root ke akhir
    temp     = arr[0];
    arr[0]     = arr[end];
    arr[end]= temp;

    // majukan end
    end -= 1;

    // lakukan penataan ulang dengan siftDown
    siftDown(arr,0,end);
    }
    }

 

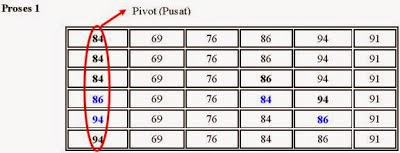
D.   - Quick Sort

Contoh dari proses Soring dengan menggunakan metode Quick Sort

Dalam Procedure Pascal :

Procedure Quick(Var Temp : Data; Awal, Akhir : Integer); 

      Var I,J : Integer; 

       Procedure ATUR; 

                   Begin 

                   I:=Awal +1; 

                   J:= Akhir; 

                    While Temp[I] < Temp[Awal] Do Inc(I);

                   While Temp[J] > Temp[Awal] Do Dec(J); 

                   While I < J Do 

                         Begin 

                                SWAP(Temp[I], Temp[J]); 

                                While Temp[I] < Temp[Awal] Do Inc(I); 

                                While Temp[J] > Temp[Awal] Do Dec(J); 

                         End; 

                   SWAP(Temp[Awal], Temp[J]); 

End; 

                  Begin 

                      If Awal < Akhir Then 

                             Begin 

                                  ATUR; 

                                  Quick(Temp, Awal, J-1); 

                                  Quick(Temp,J+1,Akhir); 

                             End; 

End;

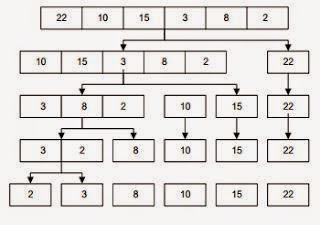
-          Merge Sort

Ilustrasi dari algoritma merge sort adalah sebagai berikut:

Algoritma mergesort(S,C)

Input: n elemen dari data S dan comparator C

Output: data S terurut berdasarkan C

if S.size()>1

(S1,S2) ← partisi(S,n/2)

mergesort(S1,C)

mergesort(S2,C)

S ← merge(S1,S2)

Fungsi merge berfungsi untuk menggabungkan hasil pengurutan dari sub

bagian S1 dan S2 berdasarkan urutan tertentu (ascending atau descending

order). Kompleksitas proses penggabungan ini (merging) adalah O(n).

Algoritma dari proses penggabungan adalah :

Algoritma merge(S1,S2)

Input: data S1 dan S2 dengan n/2 elemen per data

Output: data terurut dari penggabungan S1 È S2

S ← data kosong

while not S1.empty() and not S2.empty()

if S1.first().elemen() < S2.first().elemen()

S.insert(S1.remove(S1.first())

else

S.insert(S2.remove(S2.first())

while not S1.empty()

S.insert(S1.remove(S1.first())

while not S2.empty()

S.insert(S2.remove(S2.first())

return S

E . Shell sort (pengembangan insertion)

Contoh dari proses Sorting dengan menggunakan metode Shell Sort :

Dalam Procedure Pascal :

Procedure Shell(Var Temp : Data; JmlData : Integer); 

Var I,J, Jarak : Integer; 

        Begin 

             Jarak := JmlData Div 2; 

              While Jarak > 0 Do 

                    Begin 

                        For I:=1 To JmlData-Jarak Do 

                             Begin 

                                 J := I + Jarak; 

                                 If Temp[I] > Temp[J] Then  

                                 SWAP(Temp[I], Temp[Lok]); 

                             End; 

                             Jarak := Jarak Div 2; 

                    End; 

          End;